Soit ABC un triangle rectangle en A tel que AB = 5 cm et AC = 4 cm. Soit G un point du segment [BC] et O un point quelconque du plan distinct de G.
Question
1. Construis les symétriques A', B', C' et G' des points respectifs A, B, C et G par la symétrie de centre O.
2. Trace le triangle A'B'C'. Que peut-on dire des points B, C et G d'une part et des points B', C' et G' d'autre part ?
3. Mesure l'angle . Quelle est la nature du triangle A'B'C' ?
4. a). A l'aide d'une règle graduée mesure la longueur du segment [A'B']. Compare les longueurs des segments [AB] et [A'B'].
b). Trace les droites (AB) et (A'B'). Que peut-on dire de ces droites ?
5. Calcule et compare les aires des triangles ABC et A'B'C'.
Solution
1. Je construis :
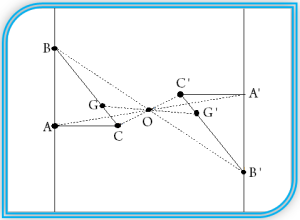
2. Je peux dire que les points B, C et G sont alignés et que les points B', C' et G' sont aussi alignés.
3. En mesurant l'angle , je trouve 90°. Le triangle A'B'C' est rectangle en A'.
4. a). En mesurant la longueur du segment [A'B'], j'obtiens 5 cm. Les segments [AB] et [A'B'] ont la même longueur.
b). Je peux dire que les droites (AB) et (A'B') sont parallèles.
5. Je calcule les aires des triangles ABC et A'B'C'.
aire(ABC) = = = 10 cm2
aire(A'B'C') = = = 10 cm2
Je conclure que : aire(ABC) = aire(A'B'C').