J'observe pour découvrir
Observe la figure géométrique et réponds aux questions.

Question
Décris cette figure et nomme-la.
Cette figure est une ligne courbe fermée.
Elle a un centre, un rayon et un diamètre comme dimensions.
C'est un cercle.
Remarque :
Le pourtour du cercle est appelé circonférence.
Le diamètre est un segment qui passe par le centre du cercle. C'est le double du rayon.
Le rayon est la distance entre le centre et un point de la circonférence.
Question
Comment construit-on le cercle ?
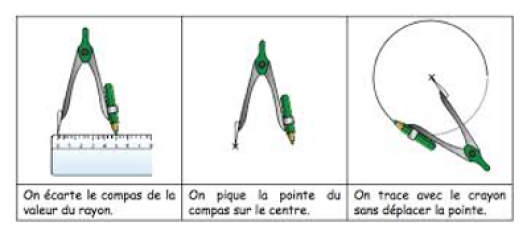
Pour tracer un cercle à l'aide du compas et de la règle, je mesure le rayon en marquant des points aux extrémités ;
ensuite, je pique la pointe du compas sur une extrémité du rayon qui sera le centre du cercle ;
enfin, je forme la circonférence avec le crayon du compas sans déplacer la pointe.
Remarque :
On peut également tracer un cercle à l'aide d'une corde et d'une pointe.
Question
Comment calcule-t-on le périmètre ou la circonférence du cercle ?
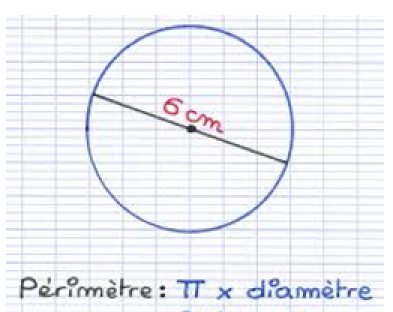
Pour calculer le périmètre du cercle on utilise un nombre invariable appelé pi. On l'écrit π.
pi = 3,14
Périmètre de ce cercle = 3,14 x 6 cm = 18, 84 cm
Périmètre du cercle = π x diamètre

On peut aussi calculer le périmètre à partir du rayon.
Périmètre de ce cercle = 3,14 x (4 cm + 4 cm) = 25,12 cm
ou encore le diamètre étant le double du rayon, périmètre de ce cercle = 3,14 x (4 cm x 2) = 25,12 cm
Périmètre du cercle ou circonférence = π x (rayon + rayon) ou π x rayon x 2 ou encore 2 x π x rayon
On écrit C = 2π x r





