Exercice d'application
Question
On considère une partie du tableau de variation de la fonction \(f\) donnée ci-dessous.
1. Donner le domaine de définition de \(f\).
2. Donner les limites de \(f\) aux bornes de son domaine de définition
3. Compléter le signe de la fonction dérivée de \(f\) dans le tableau suivant
4. \(f\) admet-elle un extremum sur \(]-\infty ; -2[\). Si oui préciser sa nature (minimum ou maximum)
5. \(f\) admet-elle un extremum sur \(] -2 ; +\infty[\). Si oui préciser sa nature (minimum ou maximum)
Solution
1. \(D_{f}=]-\infty ; -2[\bigcup ] -2 ; +\infty[\)
2.
\(\lim\limits_{x\rightarrow -\infty} f(x)=-\infty ; \lim\limits_{x\rightarrow +\infty} f(x)=+\infty ;\)
\(\lim\limits_{x\rightarrow -2^{-}} f(x)=-\infty ; \lim\limits_{x\rightarrow -2^{+}} f(x)=+\infty\)
3.
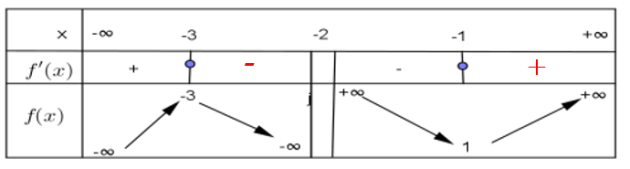
4. Sur l'intervalle \(]-\infty ; -2[\) \(f'(x)\) s'annule en changeant de signe en \(-3\) donc \(f\) admet un maximum égal à \(-3\) en \(-3\).
5. Sur l'intervalle \(] -2 ; +\infty[\) \(f'(x)\) s'annule en changeant de signe en \(-3\) donc \(f\) admet un minimum égal à \(1\) en \(-1\).