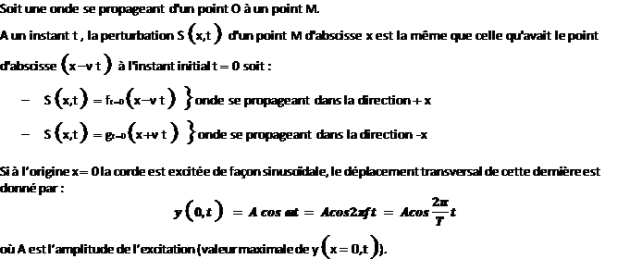Propagation d'un signal le long d'une corde
Il suffit de provoquer une secousse à l'extrémité d'une corde tendue. La déformation ainsi générée va se propager le long de la corde. La forme de cette déformation peut être quelconque.
Aspect de la corde à un instant donné
La forme de la corde à l'instant t = 0 peut être représentée par une fonction mathématique : y= f(x).
Un instant plus tard, la perturbation s'est propagée et se trouve plus loin à une position x' avec x' – x = vt où v est la vitesse de propagation de l'onde.
La vitesse de propagation d'une onde le long d'une corde est \(v = \sqrt{\frac{F}{μ}}\), F étant la tension de la corde et μ la masse linéique de la corde (masse par unité de longueur).
Équation horaire d'un point donné de la corde