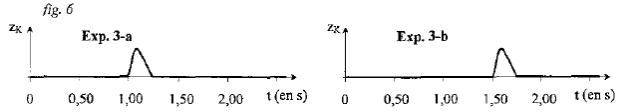2
Une très longue corde élastique inextensible est disposée horizontalement. Un opérateur crée une perturbation en imprimant une brève secousse verticale à l'extrémité S de la corde.
Question
1. Considérations générales :
- Préciser la direction de propagation et la direction du mouvement du point M.
- En déduire si l'onde est transversale ou longitudinale.
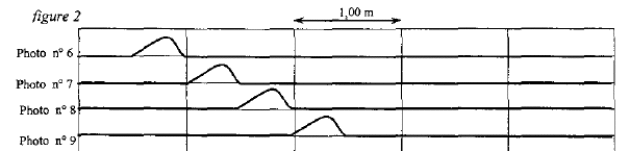
2. Étude chrono-photographique : La propagation de l'onde est étudiée par chronophotographie. L'intervalle de temps séparant deux photos consécutives est Δt = 0,25 s.
Enregistrement
- Définir puis calculer la célérité de l'onde.
- Pendant quelle durée un point de la corde est-il en mouvement ?
3. Evolution temporelle du déplacement vertical de plusieurs points de la corde : l'évolution au cours du temps des altitudes zA et zB de deux points A et B de la corde est l'objet de la figure 3 . L'instant de date t0 = 0 s correspond au début du mouvement de S. Toutes les réponses doivent être justifiées.
- Lequel de ces deux points est touché par la perturbation ?
- Lequel de ces deux points est situé le plus près du point source S ?
- Quel retard le point touché en second présente-il dans son mouvement par rapport au point touché en premier ?
- Quelle est la valeur de la distance séparant les deux points A et B ?
- Un troisième point C commence son mouvement à l'instant de date tC = 0,50 s. Préciser sa position par rapport à A.
- Représenter sur un schéma la position des points A, B et C ( échelle 2 cm pour 1 m) par rapport au point source S.
4. Influence de quelques paramètres sur la célérité de l'onde : Les courbes ci-dessous ( figures 4, 5 et 6) donnent l'évolution au cours du temps du déplacement vertical d'un point K d'une corde situé à la distance fixe d = SK du point source S ; l'instant de date t = 0 correspond au début du mouvement de S ; les conditions expérimentales sont précisées pour chaque expérience. Toutes les réponses doivent être justifiées en utilisant les représentations graphiques. On étudie successivement l'influence de la forme de la perturbation, la tension de la corde, la nature de la corde.
- Influence de la forme de la perturbation : la même corde est utilisée ; sa tension est la même dans toutes les expériences. La forme de la perturbation modifie-t-elle la célérité ?
- Influence de la tension de la corde : la même corde est utilisée ; lors de l'expérience 2a la tension est plus faible que lors de l'expérience 2b. La tension de la corde modifie-t-elle la célérité et si oui, dans que sens ?
- Influence de la nature de la corde : On rappelle que la masse linéique μ est la masse par unité de longueur ; pour une corde de masse M et de longueur L :
μ = M/L. La tension est la même dans les deux expériences ; la masse linéique de la corde utilisée expérience 3a est plus faible que celle de la corde utilisée pour l'expérience 3b. La masse linéique de la corde modifie-t-elle la célérité et si oui, dans quel sens ?
Solution
1. L'onde se propage le long de la corde placée suivant l'horizontale. La perturbation est verticale, perpendiculaire à la direction de propagation de l'onde : en conséquence, l'onde est transversale.
Je calcule la célérité de l'onde (exprimée en m/s) en divisant la distance AB (exprimée en m) parcourue par le front de l'onde par la durée correspondante (exprimée en s).
2. Les photos n°6 et n°8 indiquent que le front de l'onde parcourt une distance égale à 1 m en 2*0,25 = 0,5 s.
v = 1/0,5 = 2 m/s.
Un point de la corde est en mouvement pendant : 0,5 / 2 = 0,25 s.
3. Chaque point M de la corde reproduit le mouvement de la source S avec un retard θ = xM/ v, xM étant la distance SM du point M à la source
Or θA= 1,5 s et θB= 2 s ; θA <θB donc A reproduit le premier le mouvement de la source ;
le point B présente un retard de 0,5 s par rapport au point A qui, lui est touché en premier xA= tA.v = 1,5*2 = 3 m ; xB= θB v = 2*2 = 4 m ; A est plus proche de la source que le point B.
xB-xA= 4-3 = 1 m.
Un troisième point C commence son mouvement à l'instant de date tC = 0,50 s. En conséquence ce point est touché par le front de l'onde avant le point A : C est situé à gauche de A tel que xC= tC *v = 0,5*2 = 1 m.
4. La figure 4 indique que le front des ondes arrive au point K, au même instant t = 1,50 s. Le front de l'onde parcourt la même distance pendant le même intervalle de temps. La forme de la perturbation ne modifie donc pas la célérité de l'onde.
La figure 5 indique que :
Données : les cordes ont même masse linéique, mais n'ont pas la même tension.
le front de l'onde de l'expérience 2a arrive au point K à l'instant ta = 1,50 s .
le front de l'onde de l'expérience 2b arrive au point K à l'instant tb = 0,80 s .
Le front de l'onde atteint le point K plus rapidement dans l'expérience 2b que dans l'expérience 2a ; donc la célérité de l'onde est plus grande dans l'expérience 2b que dans l'expérience 2a.
la tension de la corde modifie donc la célérité de l'onde.
De plus, la tension de la corde est plus grande dans l'expérience 2b que dans l'expérience 2a.
La célérité de l'onde est d'autant plus grande que la tension de la corde est plus grande.
La figure 6 indique que :
Données : les cordes sont différentes (masse linéique différente), mais ont la même tension.
le front de l'onde de l'expérience 3a arrive au point K à l'instant ta = 1,00 s .
le front de l'onde de l'expérience 3b arrive au point K à l'instant de date tb = 1,50 s .
Le front de l'onde atteint le point K plus rapidement dans l'expérience 3a que dans l'expérience 3b. La célérité de l'onde est donc plus grande dans l'expérience 3a que dans l'expérience 3b.
La masse linéique de la corde modifie donc la célérité de l'onde.
De plus, la masse linéique de la corde est plus faible dans l'expérience 3a que dans l'expérience 3b.
La célérité de l'onde est d'autant plus petite que la tension de la corde est plus grande.