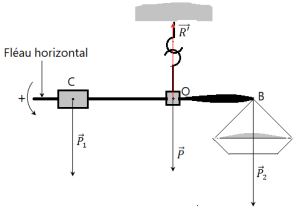
Soit une balance romaine. La partie du fléau (sans le fléau) située à gauche de l'axe passant par O équilibre exactement la parie située à droite plus le plateau vide. On place du riz dans le plateau et, pour obtenir l'équilibre, on doit donner au contrepoids C, de masse \(m=1\:kg\), une position telle que \(OC=25\:cm\).
Question
Quelle est la masse du riz sachant que la distance \(OB\) est égale à \(10\:cm\)
Intensité de la pesanteur:g = 9,8 N/kg.
Solution
Le fléau est susceptible de tourner autour d'un axe horizontal Δ passant par O et qui lui est perpendiculaire.
Lorsque le plateau est vide, les forces qui s'exercent sur le fléau sont le poids \(\vec P\) de l'ensemble du fléau (sans le contre-poids C) et du plateau vide et la réaction \(\vec R\) de l'axe de rotation sur le fléau.
Le fléau étant en équilibre, une des conditions nécessaires d'équilibre d'un solide soumis à deux forces permet de dire que \(\vec P\) et \(\vec R\) ont le même support. Comme \(\vec R\) passe par \(O\), \(\vec P\) passe aussi par \(O\).
Lorsque le plateau est chargé, les forces qui s'exercent sur le fléau sont :
le poids \(\overrightarrow {P_1}\) du contrepoids \(C\);
le poids \(\overrightarrow{P_2}\) du riz ;
le poids \(\vec P\) de l'ensemble du fléau et plateau vide ;
La réaction \(\overrightarrow {R'}\) de l'axe Δ sur le fléau.
Le fléau étant en équilibre, la somme des moments algébriques est nulle :
\(M_{\Delta}(\overrightarrow {R'})+M_{\Delta}(\overrightarrow {P_1})+M_{\Delta}(\vec P_2)+\vec P=0\)
\(M_{\Delta}(\overrightarrow {R'})=M_{\Delta}(\vec {P})=0\)
En effet,\(\overrightarrow {R'}\) et \(\vec P\) rencontrent l'axe Δ.
Avec le sens positif choisi (arbitrairement) , on a :
\(M_{\Delta}(\overrightarrow {P_2})=-P_2\cdot OB\) (\(\overrightarrow { P_2}\) tend à faire tourner le fléau dans le sens opposé au sens positif choisi)
\(M_{\Delta}(\vec {P_1})=P_1\cdot OC\) (\({\vec P_1}\) tend à faire tourner le fléau dans le sens positif choisi).
On a finalement :
\(P_1 \cdot OC-P_2 \cdot OB=0\) soit
\(P_2=\frac{P_1 \cdot OC}{OB}=\frac{m\cdot g\cdot OC}{OB}\)
La masse du riz est \(m'=\frac{P_2 }{g}=\frac{m \cdot OC}{OB}\).
\(m'=\frac{1 \times 0,25}{0,1}=2,5 \:kg\)
La masse du riz est 2,5 kg
Remarque :
\(m'=\frac{m \cdot OC}{OB}\): la masse du riz ne dépend pas de l'intensité de la pesanteur \(g\); elle ne dépend donc pas du lieu.