Definition
Définition :
La fonction logarithme népérien ln est définie sur ]0 ;+∞[ .
Elle est continue et dérivable sur ]0 ;+∞[ .
Limites en 0+ et en +∞
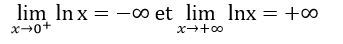
Sens de variation et tableau de variation de ln

Branches infinies

Le nombre e
La fonction ln étant bijective de ]0 ;+∞[ vers ]- ∞ ;+∞[ , le réel 1 a donc un seul antécédent par ln que l'on note e.
On appelle e l'unique antécédent de 1 par ln.
ln e =1 ; ln
 = - ln e= -1
= - ln e= -1
e est un nombre réel transcendant comme π
e=2,718281828....
e≃2,72
Quelques tangentes à la courbe
Au point d'abscisse 1
y=ln' 1(x-1)+ln1
y= x-1
Pour x = 1 ; y= 0 on a (1 ;0 )
Pour x =2 ; y=1 on a (2 ; 1 )
Au point d'abscisse e
y=ln' e(x-e)+lne
y =
 x
x
pour x=e ; y=1 on a (e ; 1 )
pour x = 2e ; y=2 on a ( 2e ;2 )





