Je peux appliquer la loi de la décroissance radioactive
Je peux appliquer la loi de la décroissance radioactive
À une date t=0, on dispose d'un échantillon contenant en moyenne N0 noyaux de polonium radioactifs 210 radioactifs. À une date t, on détermine le nombre de noyaux restants. Les mesures ont permis de dresser le table suivant :
Temps en jours (j) | 0 | 40 | 80 | 120 | 160 | 200 | 240 |
N/N0 | 1 | 0,82 | 0,67 | 0,55 | 0,45 | 0 ,37 | 0,3 |
Question
Tracer la courbe de
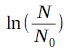en fonction du temps t.À l'aide de la représentation graphique, déduire la constante radioactive et la période du polonium 210.
Au bout de combien de temps la masse restante de polonium devient-elle le dixième de la masse initiale.
Application de la loi de décroissance radioactive
1. Représentation graphique
Temps t (jours) | 0 | 40 | 80 | 120 | 160 | 200 | 240 |
N/N0 | 1 | 0,82 | 0,67 | 0,55 | 0,45 | 0 ,37 | 0,3 |
Log (N/N0) | 0 | -0,20 | -0,40 | -0,60 | -0,80 | -0,99 | -1,20 |
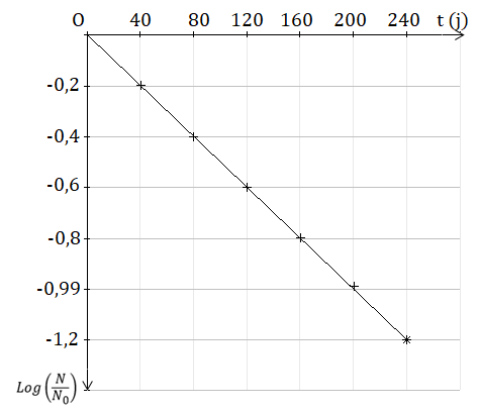
Détermination de la constante radioactive
La représentation graphique de Log(N/N0) en fonction de t est une droite.
Or Log(N/N0) = - λ.t ; Donc le coefficient directeur de la droite est - λ.
Considérons les points de coordonnées (t = 40 ; Log(N/N0 = -0,20) et (t = 240 ; Log(N/N0).
- λ =
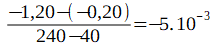
λ = 5.10-3 j-1
Détermination de la période radioactive
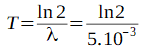= 138,6 jT = 138,6 j
3. Détermination du temps
= 
= - λ.t
t = 460,5 j
