Question

Définis un mouvement uniforme.

Solution

Mouvement uniforme.

Un mouvement uniforme est un mouvement pour lequel la valeur de la vitesse est constante.

Question

  1. Définis un mouvement curviligne.

  2. Définis un mouvement circulaire.

  3. Définis un mouvement circulaire uniforme

Solution

DéfinitionMouvement curviligne

Un mouvement curviligne est un mouvement pour lequel la trajectoire est une courbe quelconque.

DéfinitionMouvement circulaire

Un mouvement circulaire est un mouvement curviligne pour lequel la trajectoire est un cercle.

DéfinitionMouvement circulaire uniforme

Un mouvement circulaire uniforme est un mouvement pour lequel la trajectoire est un cercle et la valeur de la vitesse est constante.

Question

Définis l'abscisse curviligne

Solution

DéfinitionAbscisse curviligne

Lorsque la trajectoire d'un point mobile est connue, il est commode d'utiliser l'abscisse curviligne.

Pour définir l'abscisse curviligne :

  • on choisit sur la trajectoire un point origine,

  • on oriente la trajectoire en indiquant un sens positif de parcours.

    La position d'un point \(M\) est alors parfaitement définie par la mesure algébrique de l'arc \(\stackrel{\Huge\frown}{OM}\). La mesure algébrique de l'arc \(\stackrel{\Huge\frown}{OM}\) notée \(s\), est appelée abscisse curviligne : \(\mathbf{s= \stackrel{\Huge\frown}{OM}}\)

Soit un point mobile \(M\) dans un repère \((O ;\vec i ;\vec j)\) tel que \(\overrightarrow{OM}=\vec r\) et \(\theta=(\vec i;\overrightarrow{OM})\).

Question

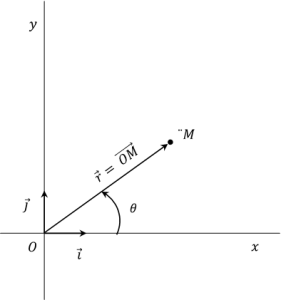
Quelles sont les relations qui permettent de passer des coordonnées polaires \((r,\theta)\) aux coordonnées cartésiennes \((x ;y)\)?

Solution

Passage des coordonnées polaires aux coordonnées cartésiennes.

Connaissant les coordonnées polaires \((r,\theta)\), ont trouve les coordonnées cartésiennes par les relations suivantes :

\(\left\{\begin{array}{cc} x=r\cos(\theta) \\ y=r\sin(\theta) \end{array} \right.\).

Question

Exprime la vitesse moyenne d'un point en utilisant l'abscisse curviligne.

Solution

\(v_m=\frac{s_2-s_1}{t'-t}\) où \(s_1\) et \(s_2\) sont les abscisses curvilignes du point aux instants respectifs \(t_1\) et \(t_2\).

Question

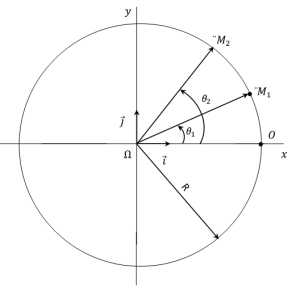
Établis la relation entre la vitesse moyenne et la vitesse angulaire moyenne d'un point en mouvement circulaire uniforme.

Solution

Relation entre vitesse moyenne et vitesse angulaire moyenne

Soit \(M_1\) et \(M_2\) les positions du point mobile aux intants respectifs \(t_1\) e \(t_2\). Les abscisses curvilignes de \(M_1\) et de \(M_2\) aux instants respectifs \(t_1\) et \(t_2\) sont respectivement :

\(s_1=R{\theta}_1\) et \(s_2=R{\theta}_2\)

\(v_m=\frac{s_2-s_1}{t_2-t_1}=\frac{R({\theta}_2-{\theta}_2)}{t_2-t_1}\)

\(\omega_m=\frac{({\theta}_2-{\theta}_2)}{t_2-t_1}\) est la vitesse angulaire moyenne.

Ainsi, \(v_m=R\omega_m\).