On étudie le mouvement d'un satellite de la planète Saturne, de masse M. Le mouvement du satellite, assimilé à un point matériel de masse m, est étudié dans un référentiel considéré comme galiléen. On admet que Saturne a une distribution de masse sphérique et que l'orbite.

Question

  1. Montrer que le mouvement du satellite est uniforme.

  2. Exprimer la vitesse v et la période T du satellite en fonction de G, r et M.

  3. Montrer que le rapport \(\frac{T^2}{r^3}\) est constant.

  4. Sachant que la période de révolution du satellite Mimas, un satellite de Saturne, est T = 22,6 heures et que le rayon orbital est r = 185 000 km, calculer la masse M de Saturne.

  5. Un autre satellite de Saturne, appelé Rhéa, a une période T' = 108,4 heures. En déduire le rayon orbital r' du satellite Rhéa.

    On donne : G = 6,67.10-11 SI

Solution

1. Montrons que le mouvement du satellite est uniforme

  • Système : le satellite de masse m

  • Référentiel d'étude : référentiel propre à la planète Saturne supposé galiléen

  • Bilan des forces : la force gravitationnelle F ⃗ widevec {F}

  • Appliquons le TEC : \(ΔE_c = W(\vec{F})\)

    D'où le mouvement du satellite est uniforme.

2. Expressions de v et T en fonction de G, r et M

Appliquons la RFD : (1)

Dans la base de Frenet, on a :

(2)

Par identification de (1) et (2), on a :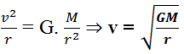

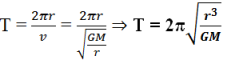
3. Montrons que est constant.

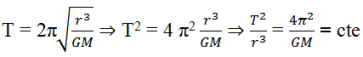
4. La masse M de Saturne

AN : M = 5,66.1026 kg

5. Le rayon orbital r

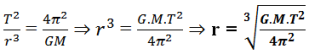
AN : r = 526116632,85 m