Fonctions croissantes-Fonctions décroissantes
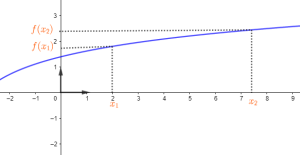
Définition : Fonctions croissantes
Soit \(f\) une fonction numérique définie sur un intervalle I de IR .
. La fonction \(f\) est croissante sur I si, pour tous réels \(x_1\) et \(x_2\) de I,
\(x_1 < x_2\)⟹ \(f(x_1)≤f(x_2)\)
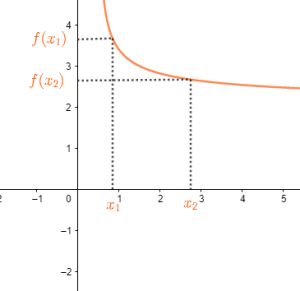
Définition : Fonctions décroissantes
. La fonction \(f\) est décroissante sur I si,
pour tous réels \(x_1\) et \(x_2\) de I,
\(x_1<x_2\)⟹\(f(x_1)≥f(x_2)\)
Remarque :
Si la fonction \(f\) est telle que :
pour tous réels \(x_1\) et \(x_2\) de I,\(x_1<x_2\)⟹\(f(x_1)<f(x_2)\) on dit que \(f\) est strictement croissante sur I.
Si la fonction \(f\) est telle que :
pour tous réels \(x_1\) et \(x_2\) de I,\(x_1<x_2\)⟹\(f(x_1)>f(x_2)\) on dit que \(f\) est strictement décroissante sur I.
Si la fonction \(f\) est telle que :
pour tous réels\( x_1\) et \(x_2\) de I,\(x_1<x_2\)⟹\(f(x_1 )=f(x_2)\) on dit que \(f\) est constante sur I.
Si une fonction est croissante sur un intervalle, ou décroissante sur un intervalle, on dit qu'elle est monotone sur cet intervalle.