Activité
Question
Soit la fonction g définie par \(g(x)=x^2+4x.\)
Déterminer le domaine de définition de \(g\).
Déterminer les limites aux bornes de ce domaine.
Calculer la dérivée \(g' (x)\) pour tout réel \(x\) de ce domaine.
Étudier le signe de \(g' (x)\) suivant les valeurs de \(x\).
Déduire les intervalles sur lesquels g est croissante ou décroissante.
Dresser le tableau de variation de \(g\).
\(g'\) s'annule-t-elle en \(-2\) ?
Que peut-on dire du signe de \(g'\) autour de \(-2\) (avant et après \(-2\))
Solution
Etudions le signe de \(g' (x)\) suivant les valeurs de \(x.\)
Déterminons le domaine de définition de \(g\).
\(D_{g}=\mathbb{R}\), car \(g\) est un polynôme.
Déterminons les limites de \(f\) aux bornes de ce domaine.
\(\begin{equation*}\lim\limits_{x\rightarrow -\infty}g(x)=\lim\limits_{x\rightarrow -\infty}(x^{2}+4x)=\lim\limits_{x\rightarrow -\infty}(x^{2})=+\infty\end{equation*}\)
\begin{equation*}\lim\limits_{x\rightarrow +\infty}g(x)=\lim\limits_{x\rightarrow +\infty}(x^{2}+4x)=\lim\limits_{x\rightarrow +\infty}(x^{2})=+\infty\end{equation*}
Calculons la dérivée \(g' (x)\) pour tout réel \(x\) de ce domaine.
\(g\) est dérivable sur \(\mathbb{R}\) et pour tout \(x∈\mathbb{R}\), on a :
\(g' (x)=2x+4\).
Etudions le signe de \(g' (x)\) suivant les valeurs de \(x\).
On a : \(2x+4≥0⟺2x≥-4\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ⟺x≥-2\)
Tableau de signe
\(x\)
\(-\infty \ \ \ \ \ \ \ \ \ -2 \ \ \ \ \ \ \ \ \ +\infty\)
\(2x+4\)
\(-\)
\(+\)
D'où pour tout \(x∈]-∞; -2] \ g'(x)≤0\) et pour tout \(x∈[-2; +∞[, g'(x)≥0\).
Déduisons les intervalles sur lesquels \(g\) est croissante ou décroissante. Les valeurs de \(g(x)\) augmentent-elles lorsque x augmente sur \(]0; +∞[ ?\)
On en déduit que : \(g\) est croissante sur \([-2; +∞[\) et décroissante sur \(]-∞; -2]\).
Dressons le tableau de variation de \(g.\)
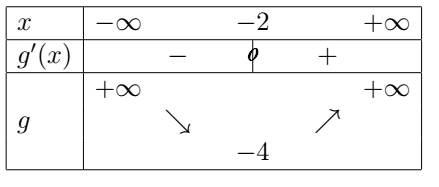
7. \(g'\) s'annule en \(-2\).
8. On peut dire que \(g'\) change de signe en \(-2\): avant \(-2\) \(g'\) est négative et après \(-2\) elle est positive.