Je découvre la méthode de construction de la la fonction définie par f(x)=sinx
Activité
Soit f la fonction définie par f(x)=sinx et ( C) sa courbe représentative dans un repère.
Question
a) Calculer sin(x+2π) , que peut – on en déduire pour la fonction f.
b) Calculer sin(-x), que peut –on en déduire pour la courbe ( C).
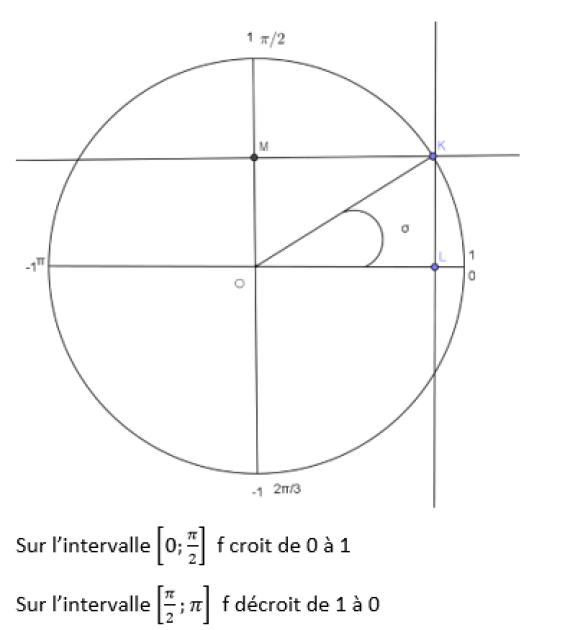
c) A l'aide du cercle trigonométrique , dresser le tableau de variation de f.
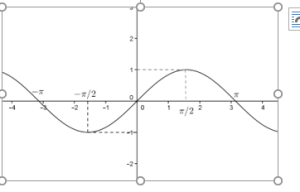
d) Construire la courbe ( C) de f
Solution
Soit f la fonction définie par f(x)=sinx et ( C) sa courbe représentative dans un repère.
a) Calculons sin(x+2π) .
sin(x+2π)=sinx donc f est périodique de période 2π.
On peut en déduire que l'étude f sur un intervalle de longueur 2π comme ⟦-π;π⟧
b) Calculons sin(-x), que peut –on en déduire pour la courbe ( C).
sin(-x)=-sinx donc f est une fonction impaire.
On peut en déduire que l'origine du repère O est un centre de symétrie à la courbe ( C) de f
c) A l'aide du cercle trigonométrique , dressons le tableau de variation de f.
D'où le tableau de variation est le suivant :
d) Construisons la courbe ( C) de f
Tableau des valeurs