Equilibre sur un plan incliné
Soit un solide de poids P connue, posé sur un plan incliné d'un angle α parfaitement lisse de manière à pouvoir négliger les forces de frottement. Ce solide est maintenu en équilibre à l'aide d'un fil parallèle à la ligne de plus grande pente.
Déterminons les intensités R et T
Appliquons la condition d'équilibre : \(\vec{P} + \vec{R} + \vec{T} = \vec{0}\)
Première méthode : méthode graphique
Faisons glisser les vecteurs forces bout à bout.
L'extrémité du dernier vecteur est confondue au point d'application du premier. Ainsi disposés les trois vecteurs constituent un triangle.
Le triangle (OAB) est rectangle en O. On en déduit les relations :
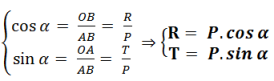
Deuxième méthode : méthode algébrique
Projetons la relation vectorielle \(\vec{P} + \vec{R} + \vec{T} = \vec{0}\) sur deux axes perpendiculaires de manière à obtenir deux relations algébriques entre les intensités des forces.
Projection sur Ox :
Le projeté \(\vec{P}_x\) de \(\vec{P}\) sur l'axe Ox est dirigé dans le sens négatif donc sa valeur algébrique Px est négative : \(sinα = \frac{{- P}_x}{P}\) ⇒ Px = - P.sinα
Le projeté \(\vec{T}_x\) de \(\vec{T}\) sur l'axe Ox coïncide avec \(\vec{T}\) , sa valeur algébrique Tx est positive : Tx = T.
La réaction \(\vec{R}\) est perpendiculaire à l'axe Ox donc son projeté sur l'axe Ox a une valeur algébrique nulle.
Projection sur Oy :
Le projeté \(\vec{P}_y\) de \(\vec{P}\) sur l'axe Oy est dirigé dans le sens négatif donc sa valeur algébrique Py est négative : \(cosα = \frac{{- P}_y}{P}\) ⇒ Py = - P.cosα
Le projeté \(\vec{R}_y\) de \(\vec{R}\) sur l'axe Oy coïncide avec \(\vec{R}\) , sa valeur algébrique Ry est positive : Ry = R.
La réaction \(\vec{T}\) est perpendiculaire à l'axe Oy donc son projeté sur l'axe Oy a une valeur algébrique nulle.
La condition d'équilibre s'écrit alors : 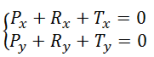
![]()
![]()
![]()