Sur une route, deux voitures roulent sur une même file avec une vitesse de \(40 \:m.s^{-1}\). Le pare-choc avant A de la seconde voiture est à \(40 m\) derrière le pare-chocs arrière B de la première voiture.
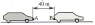
Le conducteur de la première voiture freine, soumettant son véhicule à une décélération constante de \(5 m.s^{-2}\). Le deuxième conducteur, distrait, commence à freiner 2 secondes après le premier et son véhicule subit la même décélération.
Question
Quelle distance parcourt le deuxième véhicule avant de commencer à freiner ?
Quelle distance parcourt le premier véhicule pendant ce même temps ?
Quelle est la distance séparant A et B lorsque le second véhicule commence à freiner ?
Quelle est la vitesse du premier véhicule à ce moment ?
En prenant comme origine des dates l'instant où débute le freinage du second véhicule et comme origine des espaces la position où il se trouve, établir les équations horaires des mouvements de A et de B.
Un choc aura-t-il lieu ? Si oui, à quelle date ?
Solution
1. Distance parcourue par le deuxième véhicule.
Avant de commencer à freiner, le mouvement du deuxième véhicule est rectiligne uniforme.
Prenons comme origine des dates, l'instant où commence à freiner le premier véhicule et comme origine des espaces la position du deuxième véhicule à cet instant.
\(v_0=40\:m.s^{-1}\); \(x_0=0\)
\(x=v_0t+x_0=40\times 2+0= 80\: m\).
La distance parcourue par le deuxième véhicule en 2 secondes est 80 m.
2. Distance parcourue par le premier véhicule
Le mouvement du premier véhicule est uniformément retardé pendant les deux secondes.
Prenons comme origine des espaces la position du premier véhicule à l'instant où il a commencé à freiner et comme origine des dates , cet instant : \(a_0=-5\:m.s^{-2}\); \(v_0=40\:m.s^-1\); \(x_0=0\)
\(x=\frac{1}{2}(-5)\times2^2+40\times2=70\:m\)
Pendant les 2 secondes le premier véhicule qui freinait déjà a parcouru 70 m.
3. Prenons comme origine des espaces, la position du deuxième véhicule à l'instant où le premier véhicule commence à freiner.
L'abscisse du premier véhicule au moment où le deuxième véhicule commence à freiner est : 40+70 = 110 m.
L'abscisse du deuxième véhicule à cet instant est 80 m.
La distance qui sépare A et B est 110 m - 80 m = 30 m.
4. Vitesse du premier véhicule
Prenons comme origine des espaces, l'instant où le premier véhicule commence à freiner et comme origine des dates, cet instant ; \(a_0=-5\:m.s^{-2}\); \(v_0=40\:m.s^{-1}\);\(x_0=0\).
\(v=a_0t+v_0=(-5)\times 2+40=30\:m.s^{-1}\)
La vitesse du premier véhicule est \(30\:m.s^{-1}\)
5. Équations horaires
À partir de l'instant où le deuxième véhicule commence à freiner, les deux véhicules ont un mouvement rectiligne uniformément retardé.
Pour le premier véhicule : \(a_0=-5\:m.s^{-2}\); \(v_0=30 \:m.s^{-1}\); \(x_0=40 \:m\).
\(x_B=\frac{1}{2}(-5)t^2+30t+30\)
\(x_B=-2,5t^2+30t+30\)
Pour le deuxième véhicule : \(a_0=-5\:m.s^{-2}\); \(v_0=40 \:m.s^{-1}\); \(x_0=0 \).
\(x_A=\frac{1}{2}(-5)t^2+40t\).
\(x_A=(-2,5)t^2+40t\)
5. Possibilité de choc
Il y a choc si l'équation \(x_A=x_B\) a une solution physiquement acceptable c'est-à-dire \(t\ge0\)
La solution de cette équation est \(t=3\:s\).
Il y aura un choc à la date \(t=3\:s\).