Résonance d'intensité

La courbe de résonance : Description de l'expérience

Soit le schéma du montage ci-contre :

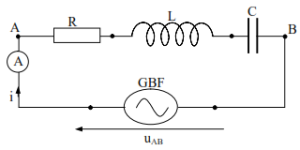
La tension efficace U du GBF étant fixée, on fait varier sa fréquence N et on note les valeurs de l'intensité efficace I du courant qui circule dans le circuit RLC. Les résultats des mesures figurent dans le tableau ci-dessous.

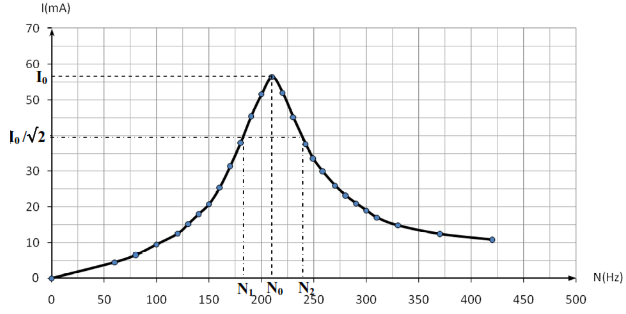
Ces mesures permettent de tracer la courbe ci-dessous.

Courbe de résonance

Interprétation

Soit U la tension fournie par le générateur : U = Z.I ou I = U Z I = {U} over {Z} .

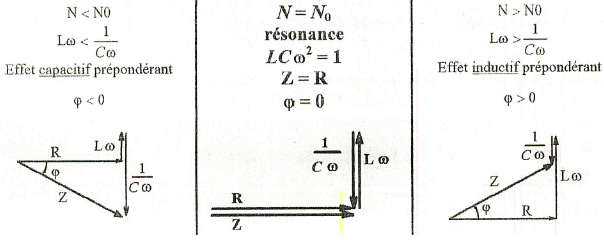
Lorsque Z prend une valeur faible ; I prend une valeur plus élevée. Au minimum R = Z si L . ω = 1 C . ω L. %omega = {1} over {C. %omega } avec ω= ω0 appelé pulsation propre (N=N0)

Il y a résonance lorsque la valeur de la tension excitatrice fournie par le générateur est égale à la fréquence propre du dipôle RLC.

A la résonance, le facteur de puissance est 1 c'est-à-dire φ=0 donc u et i sont en phase.

Cas particuliers :

ComplémentBande passante à 3 décibels

Elle caractérise la largeur de la courbe de résonance. C'est aussi l'intervalle de fréquence pour lequel le dipôle RLC échange au moins la moitié de l'énergie qu'il échange à la résonance

Δ N = N 2 − N 1 = R 2 π L %DELTA N = N_{2} - N_{1} = {R} over {2 %pi L}

La largeur de la bande passante est aussi donnée par la relation Δ ω = ω 2 − ω 1 = R L %DELTA %omega = %omega _{2} - %omega _{1} = {R} over { L}

Remarque

Le facteur de qualité d'un circuit RLC mesure l'acuité de la résonance : Q = N 0 Δ N = 2 π L N 0 R Q = {N}_{0} over { %DELTA N}= {2 %pi L N_{0}} over {R}

A la résonance, la tension efficace aux bornes du condensateur ou de la bobine peut être beaucoup plus grande que celle délivrée par le générateur : UC = UL = Q.U