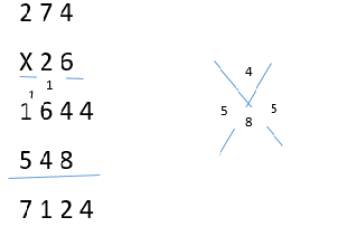Je retiens.
Multiplication des nombres entiers : preuve
1. la preuve.
la preuve de la multiplication permet de vérifier si l'opération est juste ou non.
Elle se conçoit de la façon suivante :
On trace deux lignes obliques en croix.
Comment fait-on la preuve d'une multiplication.
Dans une preuve le chiffre 9 est toujours égale à zéro. 9 = 0
On doit effectuer la multiplication avant de faire la preuve.
Quand on a fini d'effectuer la multiplication, on fait la somme des chiffres du multiplicande tout en considérant que le chiffre 9 = 0. on place le chiffre obtenu dans l'angle d'en haut du schéma.
On fait de même avec les chiffres du multiplicateur et on place le chiffre obtenu dans l'angle d'en bas.
On multiplie le chiffre obtenu du multiplicateur par celui du multiplicande tout en considérant toujours que
9 = 0. On place le chiffre obtenu dans l'angle gauche du schéma.
On additionne enfin les chiffres du produit et on place le chiffre obtenu dans l'angle droit du schéma.
Le chiffre de l'angle gauche et celui de l'angle droit doivent être égaux.
Suivons l'exemple ci-dessous ;
-multiplicande : 2 + 2 = 9. 9 = 0 ; 0 + 4 = 4
-multiplicateur : 2 + 6 = 8
4 x 8 = 32 ; 32 = 3 et 2 = 5 ;
Produit : 7 + 1 + 2 +4 = 14 ; 14 + 1 et 4 = 5
L'opération est juste.
Exemple :