Choc mou entre deux solides

Méthode

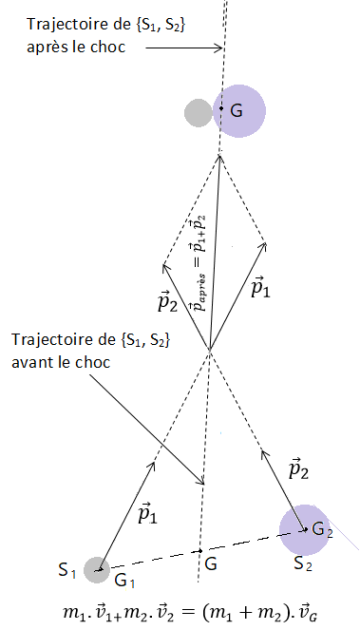
Deux solides S1 et S2 de masses respectives m 1 m_{1} et m 2 m_{2} se déplacent sans frottement sur un plan horizontal avec les vitesses respective \({\vec v}_1\) et \({\vec v}_2\). En un point du plan, ils se rencontrent et se lient pour former un solide S de masse \(m_1+m_2\)+.

Déterminons les caractéristiques du mouvement de S.

Les solides S1 et S2 interagissent au moment du choc mais ces interactions se compensent et le système {S1,S2} reste pseudo-isolé :

\({\overrightarrow p}_{avant} = {\overrightarrow p}_{apr\grave e s}\); p ⃗ avant = p ⃗ 1 + p ⃗ 2 = m 1 ⋅ v ⃗ 1 + m 2 ⋅ v ⃗ 2 {vec p} _{avant} = {vec p} _1+{vec p} _2= m_{1} cdot {vec v }_1+m_{2} cdot {vec v} _2

Le système constitué par S1 et S2 restant pseudo-isolé pendant toute la durée du mouvement, son centre d'inertie a un mouvement rectiligne uniforme. Le prolongement de la trajectoire du centre d'inertie après le choc indique la trajectoire du centre d'inertie avant le choc.

Dans le cas simple où le solide S2 est immobile avant le choc, nous pouvons déterminer facilement la vitesse v ⃗ widevec {v} du système après le choc :

p ⃗ avant = p ⃗ 1 = m 1 ⋅ v ⃗ 1 {vec p} _{avant} = {vec p}_1=m_{1} cdot {vec v} _1 ; \({\overrightarrow p}_{apr\grave e s}=(m_1+m_2) \cdot \overrightarrow v\).

\({\overrightarrow p}_{avant} = {\overrightarrow p}_{apr\grave e s}\) et m 1 . v ⃗ 1 = ( m 1 + m 2 ) ⋅ v ⃗ ⇒ v ⃗ = m 1 ( m 1 + m 2 ) v ⃗ 1 m_{1}.{vec v} _1 = (m_{1}+m_{2}) cdot vec v drarrow vec v= {m_{1}} over {(m_{1}+m_{2})} {vec v}_1