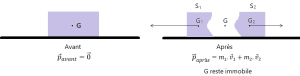
Éclatement d'un solide en deux morceaux [Applications du principe de l'inertie]

Éclatement d'un solide en deux morceaux

Méthode : Éclatement d'un solide en deux morceaux

Un solide pseudo-isolé S, de masse m,immobile par rapport au référentiel du laboratoire (considéré comme galiléen) éclate en deux solides S₁et S₂ de masses respectives $m_{1}$ et $m_{2}$ . Les deux solides se déplacent avec les vitesses respectives ${\vec{v}}_{1}$ et ${\vec{v}}_{2}$ .

Déterminons les caractéristiques des mouvements de S₁ et de S₂.

Les systèmes {S₁,S₂} ou {S} sont pseudo_isolés. Leurs vecteurs quantité de mouvement sont égaux.

La quantité de mouvement de {S} est ${\vec{p}}_{avant} = \vec{0}$

La quantité de mouvement de {S₁,S₂} est ${\vec{p}}_{après} = m_{1} \cdot {\vec{v}}_{1} + m_{2} \cdot {\vec{v}}_{2}$

${\overrightarrow p}_{avant} = {\overrightarrow p}_{apr\grave e s}$ soit $m_{1} \cdot {\vec{v}}_{1} + m_{2} \cdot {\vec{v}}_{2} = \vec{0}$ ou $m_{1} \cdot {\vec{v}}_{1} = - m_{2} \cdot {\vec{v}}_{2}$ .

Après l'éclatement les solides S₁ et S₂ se déplacent suivant la même direction mais dans des sens opposés.

Les valeurs de ${\vec{v}}_{1}$ et de ${\vec{v}}_{2}$ sont telles que $m_{1} \cdot v_{1} = m_{2} \cdot v_{2}$ .

On alors $\frac{v_{1}}{v_{2}} = \frac{m_{2}}{m_{1}}$ : la vitesse d'un morceau après l'éclatement est inversement proportionnelle à sa masse c'est-à-dire que le solide de masse plus élevée a la vitesse la plus faible.