Moment d'un couple de forces [Physique 2des C, T : Équilibre d'un solide mobile autour d'un axe fixe]

Moment d'un couple de forces

Définition : Couple de forces

On appelle couple de forces un ensemble de deux forces parallèles de même intensité, de sens opposés et n'ayant pas le même support.

Les deux forces sont contenues dans un plan appelé plan du couple.

Remarque :

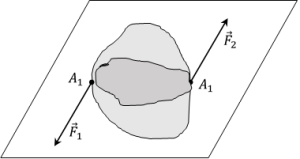
Un couple de forces peut être défini comme un ensemble de deux forces de somme vectorielle nulle et n'ayant pas le même support .

Moment d'un couple de forces

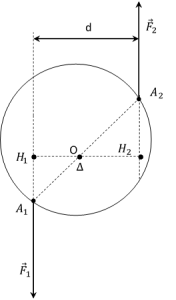
Envisageons le cas d'un couple de forces pour lequel le plan du couple est perpendiculaire à l'axe de rotation $\Delta$. Chaque force est alors perpendiculaire à l'axe de rotation. Notons $M_{Δ} (\vec{F_{1}}, \vec{F_{2}})$ , le moment du couple.

$M_{\Delta}({\vec F}_1 , {\vec F}_2)=M_{\Delta}({\vec F}_1)+M_{\Delta}({\vec F}_2)=F_1 \times OH_1 + F_2 \times OH_2$.

Notons $F$ l'intensité commune de $\vec{F_{1}}$ et de $\vec{F_{2}}$ : $F = F_{1} = F_{2}$ .

$M_{Δ} (\vec{F_{1}}, \vec{F_{2}}) = F ({OH}_{1} + {OH}_{2})$ .

${OH}_{1} + {OH}_{2} = d$ , on a finalement :

$M_{Δ} (\vec{F_{1}}, \vec{F_{2}}) = F \times d$

$M_{Δ} (\vec{F_{1}}, \vec{F_{2}})$ : moment du couple de forces en newton mètre ((N.m) ;

$F$ : intensité de l'une des forces du couple en newton (N) ;

$d$ : distance entre les supports des forces ou distance de bras de levier en mètre (m).

Ainsi, le moment d'un couple de forces est indépendant de la position de l’axe de rotation. Il ne dépend que de l'intensité de l'une des forces et de la distances entre les supports des forces.

Fondamental : Théorème des moments

Lorsqu'un solide mobile autour d'un axe et soumis à un ensemble de n actions mécaniques est en équilibre autour de cet axe, alors nécessairement la somme des moments algébriques est nulle : $M_{1} + M_{2} + M_{3} + ... + M_{n} = 0$ ; $M_{1}, M_{2}, M_{3}, \dots, M_{n}$ étant les moments algébriques.

Cette relation s"écrit aussi : $\sum\limits_{i=1}^{n}M_i=0$.

Remarque :

La condition nécessaire précédente n'est pas suffisante. En effet même lorsqu'elle est vérifiée, le solide peut être effectivement en équilibre autour de l'axe ou être en mouvement de rotation uniforme autour de l'axe.