3
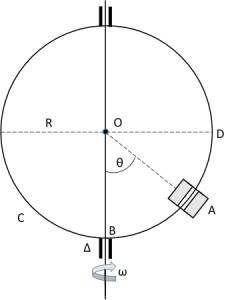
Un anneau A peut glisser sans frottement le long d'un contour circulaire C vertical, de centre O et de rayon R = 0,4 m (figure ci-contre).
La masse de l'anneau vaut M = 20 g et celui-ci est supposé indéformable. On fait tourner C autour d'un axe vertical Δ à raison de 2 tr.s-1 (tours par seconde) ; l'anneau s'écarte alors de l'axe Δ et « s'immobilise » alors en A, tel que .
Question
Calculer la valeur de θ.
À quelle vitesse maximale, exprimée en tr.s-1, le cercle C doit-il tourner pour que l'anneau A puisse s'éloigner du point B ?
Est-il possible que l'anneau se positionne en D, situé sur l'horizontale de O ?
Solution
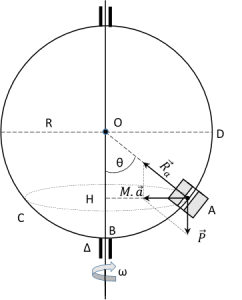
L'anneau est soumis à son poids \(\vec P\) et à la réaction \({\vec R}_a\).
1. Calcul de \(\theta\)
Appliquons le principe fondamental de la dynamique à l'anneau : \(\vec P+{\vec R}_a=M \cdot \vec a \).
Une relation trigonométrique dans un triangle rectangle permet d'écrire :
\(\tan\theta=\frac{M\cdot a_n}{P}\) avec \(a_n=AH\cdot{\omega}^2\) et \(P=M \cdot g\)
\(\tan\theta=\frac{(MR\sin\theta){\omega}^2}{M \cdot g}\) soit \(\cos\theta= \frac{g}{R \cdot {\omega}^2}\) ave c\(\omega=2\pi N\).
\(\cos\theta=\frac{9,8}{0,4 \times {(2\pi \times 2)}^2}\).
\(\theta=81,07°\).
2. Calcul de la vitesse minimale \(N_m\)
\(\cos\theta < 1 \implies \omega > \sqrt{\frac{g}{R}}\).
\({\omega}_m=\sqrt{\frac{g}{R}}\)
\(N_m=\frac{{\omega}_m}{2\pi}=\frac{1}{2\pi}\sqrt{\frac{g}{R}}\).
\(N_m=\frac{1}{2\pi}\sqrt{\frac{9,8}{0,4}}=0,79 \:tr.s^{-1}\)
Si l'anneau se positionne en D, \(\theta=\frac{\pi}{2}\) et \(\cos\theta=0\). Comme \(g\ne0\),\( \frac{g}{R \cdot {\omega}^2}\ne 0\): l'anneau ne peut pas se positionner en D.
Autre raisonnement : en D, \({\vec R}_a \)est horizontal (il est porté par(OD)). Sa composante verticale est nulle : aucune force ne s'oppose à \(\vec P\) et l'anneau descend sous l'action de \(\vec P\).