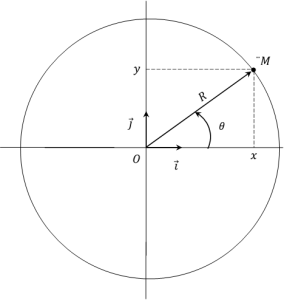
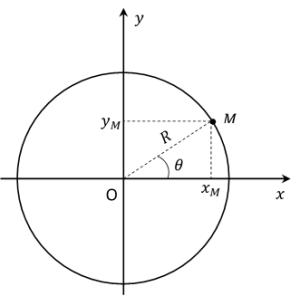
Équations horaires d'un mouvement circulaire uniforme
La vitesse instantanée \(v\) est la vitesse moyenne \(v_m=\frac{R({\theta}_2-{\theta}_2)}{t_2-t_1}\) calculée pour \(t_2\) très proche de \(t_1\):
La vitesse angulaire instantanée est :
Par définition de la dérivée, .
La vitesse instantanée est alors : \(v=R\omega\).
Pour un mouvement circulaire uniforme, \(v\) est une constante. \(\omega\) est donc aussi une constante : \(\omega=\omega_0=\frac{d\theta}{dt}\); \(\omega_0\) étant une constante.
\(\theta\) est une primitive de \(\omega_0\): \(\theta=\omega_0 \cdot t+C\) avec \(C\), une constante.
Supposont qu'à \(t=0\), on ait \(\theta=\theta_0\). On alors \(C=\theta_0\) et finalement ; \(\theta={\omega_0}t+\theta_0\)
Ainsi les équations horaires d'un mouvement circulaire uniforme sont :
Si à \(t=0\), le point \(M\) est sur l'axe Ox, on a \(\theta_0=0\).