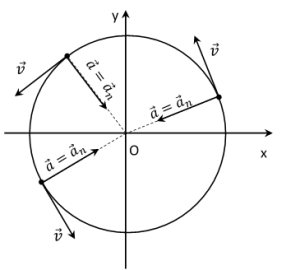
Expression de l'accélération
Dans un mouvement circulaire uniforme, la trajectoire du mobile est un cercle et la valeur \(v\) de la vitesse est constante.
L'expression du vecteur accélération en fonction des vecteurs unitaires de la base de Frenet est : . La valeur \(v\) de la vitesse étant une constante, \(\frac{dv}{dt}=0\) et la composante \(\vec {a}_t = \frac{dv}{dt}\cdot \vec {u}=\vec 0\). Le vecteur accélération \(\vec a\) se réduit à sa composante normale \(\vec a_n\) :
\(\vec a = \vec a_n=\frac{v^2}{R}\cdot\vec n\)
En désignant par \(\omega=\frac {v}{R}\) la vitesse angulaire, \(R\) le rayon de la trajectoire du mobile, on obtient une autre expression du vecteur accélération d'un mouvement circulaire uniforme : \(\vec a=R\omega^2.\vec n\)