Mouvement rectiligne uniforme

DéfinitionMouvement rectiligne uniforme

Un mobile est en mouvement rectiligne uniforme dans un repère donné si sa trajectoire est une droite ou une portion de droite et si son vecteur vitesse reste constant.

Méthode

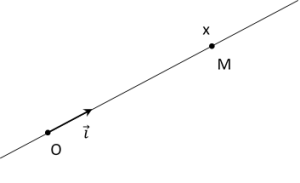
Le repère le plus simple pour étudier un mouvement rectiligne est un repère \((O ;\vec {i})\) . Le mouvement dans ce repère est alors unidimensionnel.:

OM ⃗ = x ⋅ i ⃗ v ⃗ = d OM ⃗ dt = dx dt ⋅ i ⃗ {widevec OM}=x cdot vec i newline vec v= {d widevec OM} over {dt}=dx over dt cdot vec i newline

Le vecteur \(\vec {v}\) a la même direction que \(\vec {i}\). On peut alors écrire que \(\vec {v}=v.\vec {i}\).

\(\vec {v}\) étant un vecteur constant, \(\vec{v}=\vec{v}_0=v_0\cdot i\)

On alors \(\frac {dx}{dt}\cdot\vec{i}=v_0\cdot\vec{i}\).

\(\frac{dx}{dt}=v_0\) : \(x\) est une primitive de \(v_0\). On obtient alors \(x=v_0\cdot t+ C_1\) où \(C_1\) est une constante à déterminer.

Supposons qu'à \(t=0\), le mobile soit en M0(\(x_0\)) : \(x(t=0)=x_0\) permet d'écrire que \(v_0 \times 0+C_1=x_0\) soit \(C_1=x_0\).

On obtient finalement : \(x=v_0\cdot t+x_0\).

L'équation horaire d'un mouvement rectiligne uniforme se déroulant sur un axe Ox est donc : \(\mathbf{x=v_0\cdot t+x_0}\).

On vérifie que a ⃗ = d 2 OM ⃗ dt 2 = d 2 x dt 2 ⋅ i ⃗ = 0 ⃗ vec a = {{d^2}widevec OM} over {dt^2} ={{d^2} x} over {dt^2} cdot vec i=vec 0 : le vecteur accélération d'un mobile en mouvement rectiligne uniforme est un vecteur nul.