Mouvement rectiligne uniformément varié

DéfinitionMouvement rectiligne uniformément varié

Un mobile est en mouvement rectiligne uniformément varié si sa trajectoire est une droite ou une portion de droite et si son vecteur accélération reste constant.

MéthodeÉquations cinématiques du mouvement

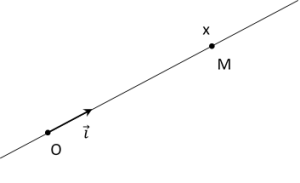
Le repère le plus simple pour étudier un mouvement rectiligne est un repère \((O ;\vec {i})\) .. Le mouvement dans ce repère est alors unidimensionnel.:

OM ⃗ = x ⋅ i ⃗ v ⃗ = d OM ⃗ dt = dx dt ⋅ i ⃗ {widevec OM}=x cdot vec i newline vec v= {d widevec OM} over {dt}=dx over dt cdot vec i newline

Le vecteur \(\vec {v}\) a la même direction que \(\vec {i}\). On peut alors écrire que \(\vec {v}=v.\vec {i}\)

a ⃗ = d v ⃗ dt = d v dt ⋅ i ⃗ vec a ={d vec v} over dt={{{ d}v} over dt} cdot vec i

a ⃗ = a 0 ⃗ = a 0 ⋅ i ⃗ vec a=widevec a_0=a_0 cdot vec i , le vecteur a 0 ⃗ widevec a_0 étant un vecteur constant.

a ⃗ = a 0 ⃗ ⇒ dv dt ⋅ i ⃗ = a 0 ⋅ i ⃗ vec a = widevec a_0 drarrow {dv} over {dt} cdot vec i={ a}_0 cdot vec i

\(\frac{dv}{dt}=a_0\).

\(v\) est alors une une primitive de \(a_0\): \(v=a_0.t+C_1\) , \(C_1\) étant une constante à déterminer.

Supposons qu'à \(t=0\), la vitesse soit connue et égale a  \(v_0\): \(v(t=0)=v_0\); \(v_0={a_0}\times {0}+C_1\) soit \(C_1=v_0\).

On obtient alors : \(v=a_0.t+v_0\) .

v ⃗ = v ⋅ i ⃗ ⇒ dx dt ⋅ i ⃗ = v ⋅ i ⃗ dx dt = v vec v = v cdot vec i drarrow dx over dt cdot vec i=v cdot vec i newline dx over dt=v

\(x\) est alors une primitive de \(v\) : x = 1 2 a 0 ⋅ t 2 + v 0 ⋅ t + C 2 x= {1} over {2} a_0 cdot {t^2}+{v_0} cdot t+{C}_2

Supposons qu'à  \(t = 0\), le solide soit en M0(\(x_0\)) : x ( t = 0 ) = 1 2 a 0 × 0 2 + v 0 × 0 + C 2 = x 0 x(t=0)= {1} over {2} a_0 times {0^2} +{v_0} times 0 +{C}_2=x_0 soit \(C_2=x_0\).

On obtient finalement : x = 1 2 a 0 ⋅ t 2 + v 0 ⋅ t + x 0 x= {1} over {2} a_0 cdot {t^2}+{v_0} cdot t+x_0

Ainsi, l'équation horaire d'un mouvement rectiligne uniformément varié est :

x = 1 2 a 0 ⋅ t 2 + v 0 ⋅ t + x 0 x= {1} over {2} a_0 cdot {t^2}+{v_0} cdot t+x_0

Les équations cinématiques d'un mouvement rectiligne uniformément varié sont :

  • équation horaire de la vitesse : \(\mathbf{v=a_0.t+v_0}\)

  • équation horaire du mouvement : x = 1 2 a 0 ⋅ t 2 + v 0 ⋅ t + x 0 x= {1} over {2} a_0 cdot {t^2}+{v_0} cdot t+x_0 \(\mathbf{x=\frac{1}{2} a_0 \cdot t^2+v_0 \cdot t +x_0}\).

    Remarque : les valeurs de \(x\), \(x_0\), \(v_0\) et de \(a_0\) sont algébriques c'est-à-dire qu'elles peuvent être positives ou négatives.

RemarqueRelation indépendante du temps

L'équation horaire d'un mouvement rectiligne uniformément varié est : x = 1 2 a 0 ⋅ t 2 + v 0 ⋅ t + x 0 x= {1} over {2} a_0 cdot {t^2}+{v_0} cdot t+x_0 .

et \(v=a_0.t+v_0\) .

\(v^2={a_0}^2t^2+2{v_0}{a_0}t+{v_0}^2\)

\(v^2-v_0^2={a_0}({a_0}t^2+2{v_0t})\).

\(x-x_0=\frac{1}{2}a_0t^2+v_0t\)

On constate que \(v^2-v_0^2=2a_0(x-x_0)\).

Une relation indépendante du temps est : \(\mathbf{v^2-v_0^2=2a_0(x-x_0)}\)