II. MONOSTABLE A AMPLIFICATEUR OPERATIONNEL
1. Exemple de montage à étudier
Notre étude portera sur le montage de la figure 2 ci-dessous dans lequel l'amplificateur opérationnel sera supposé idéal.
R = 22 kΩ
C = 10 nF
Alimentation : ±Vcc = ±12V

A l'état stable, Ve = E1 = -E = -Vsat/2 = -6 V
2. Les chronogrammes
Les chronogrammes des tension E+, uc, Vs et Ve en concordance de temps sont représentés dans la figure 3 ci-dessous
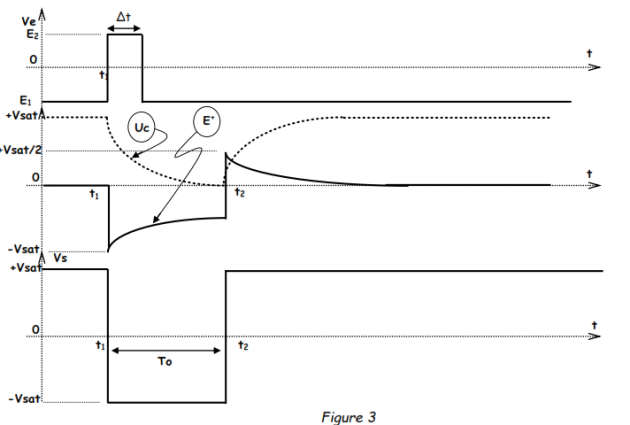
3. Interprétation des chronogrammes de la figure 3
3.1. Étude de l'état stable
Le montage est dans l'état stable tel que les potentiels n'évoluent plus : Uc = constante, ic = 0, E+ = 0, Ve = E- = E1 = -Vsat/2. (sur les chronogrammes)
Vd = E+ - E- = 0 – (-Vsat/2) = Vsat/2 > 0, donc Vs = +Vsat. Le condensateur est chargé à +Vsat. Pour faire commuter l'amplificateur opérationnel, il faudra que Vd devienne négative, donc E+ < E-, c'est à dire que Ve doit devenir positive (Ve = E2).
En résumé : État stable : Ve = E1 < 0 ; E+ = 0 ; Vd = > 0 ; Vs = +Vsat et uc = +Vsat.
3.2. Étude de l'état instable :
Le monostable est déclenché avec une impulsion : Ve = E2 > 0 pendant Δt << T0.
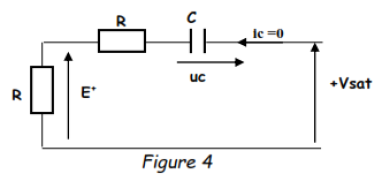
A l'instant t1, Ve = E- devient positive, Ve = E2, Vd = E+ - E- est négative et l'amplificateur opérationnel commute : Vs passe de +Vsat à -Vsat et subit une variation de -2Vsat. Cette variation est reportée sur l'autre armature du condensateur et se répartit sur les deux résistances R : E+ passe de zéro à -Vsat.
Pour t = t1+, Ve est revenue au niveau E1 = -Vsat/2 et E+ = -Vsat. Vd est devenue négative et Vs reste égale à -Vsat.
Le circuit de décharge du condensateur est représenté sur la figure 5 :
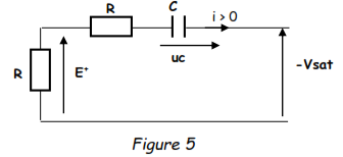
Pour t > t1, le condensateur se décharge exponentiellement à travers les deux résistances R donc avec une constante de temps τ = 2RC. E+ croît exponentiellement depuis -Vsat vers zéro.
A t = t2, lorsque E+ atteint E1 = -Vsat/2, Vd devient positive et l'amplificateur opérationnel commute : Vs passe de -Vsat à +Vsat, elle varie de +2Vsat. Cette variation est reportée sur l'autre armature du condensateur, chaque résistance R en supporte la moitié ; E+ passe de -Vsat/2 à (-Vsat/2) + (+Vsat) = +Vsat/2.
3.3. Étude de la phase de récupération
A l'instant t2, le circuit de charge du condensateur est le suivant :
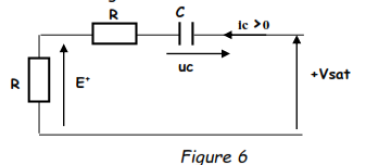
A t = t2+, on a E+ = (-Vsat/2) + (+Vsat) = +Vsat/2 et E- = Ve = -Vsat/2 ; Vd > 0, Vs reste égale à +Vsat.
Pour t > t2, le condensateur C se charge à travers les deux résistances R, donc avec une constante de temps τ= 2RC. E+ décroît exponentiellement depuis (-Vsat/2) + (+Vsat) = +Vsat/2 vers zéro.
E+ est toujours supérieure à E-, il n'y a plus de commutation possible pour l'amplificateur opérationnel. On retrouve l'état stable.
3.4. Calcul de la durée propre To
Appliquons la propriété fondamentale de la fonction exponentielle à E+ sur l'intervalle (t2 ; t1) Avec Uf = 0 ; Ui = -Vsat ; U0 = E1 = -Vsat/2. Ce qui donne :
3.5. Calcul de la durée TR de la phase de récupération
Le condensateur doit se décharger totalement (uc = +Vsat). Pour uc = 0,95.Vsat (on suppose que le condensateur est alors totalement chargé à Vsat) on à alors : ![]()
3.6. Vidéo de simulation





