III. MONOSTABLE A PORTES LOGIQUES CMOS
1. Exemple du montage à étudier
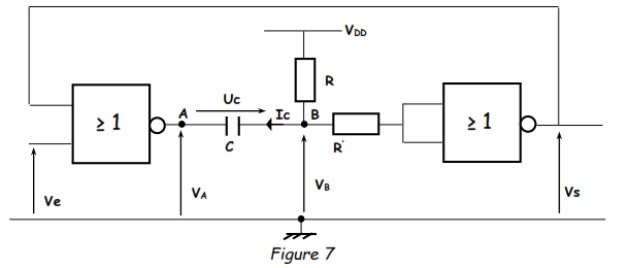
Notre étude portera sur le montage de la figure 7 ci-dessous :
Les portes NOR présentes dans le montage ont les caractéristiques suivantes :
Caractéristique de la porte (inverseuse) CMOS (le circuit est alimenté entre VDD et la masse)
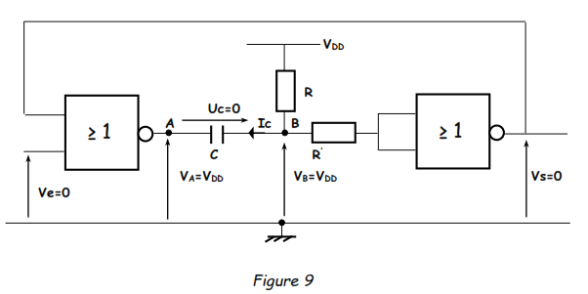
2. Fonctionnement du montage de la figure 7
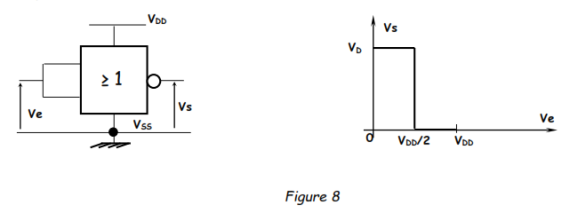
2.1 Étude de l'état stable (figure 8 ci-dessous)
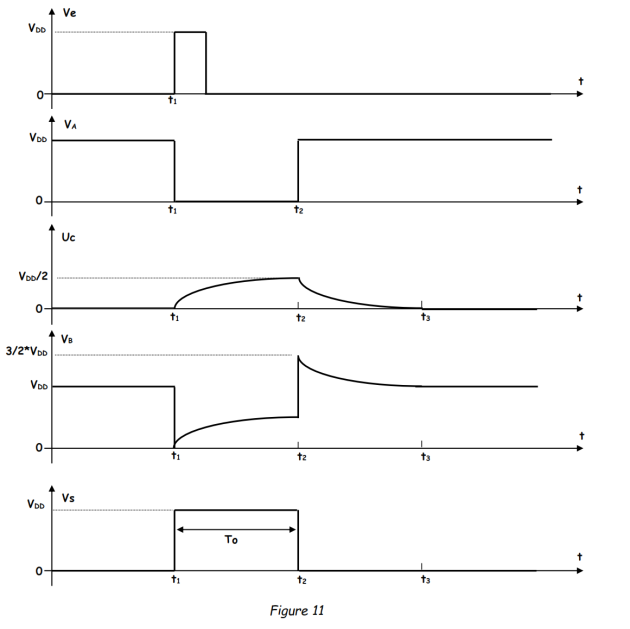
Le montage est dans l'état stable tel que les potentiels n'évoluent plus : Uc = constante et Ic = 0 → VB = VDD → Vs = 0 → VA = VDD et Ve = 0. Le condensateur est déchargé (Uc = 0).
Pour basculer à l'état instable, il faut que Ve passe au niveau logique 1 (Ve > ½VDD) pendant un temps Δt << T0
2.2. Étude de l'état instable
A l'instant t1, Ve = VDD → VA = 0 →VB = 0 (puisque la même variation de tension s'opère sur les deux armatures du condensateur).
VB = 0 → Vs = VDD →VA = 0.
Pour t = t1+, Ve est revenue zéro ; ce qui ne change pas l'état de VA. Le condensateur se charge ; de zéro, Uc va croître vers VDD.
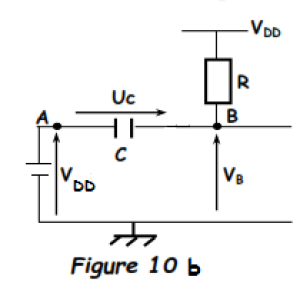
Le circuit de charge |  |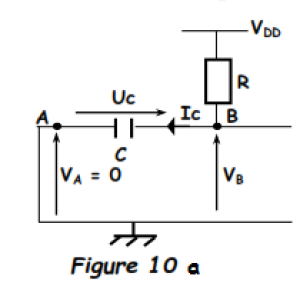
Pour t > t1, le condensateur se charge exponentiellement à travers la résistance R donc avec une constante de temps
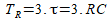. Uc et VB croissent exponentiellement de zéro vers VDD.
A t = t2, lorsque VB atteint VDD/2, Vs bascule de VDD à zéro ; or Ve était à zéro ; ce qui entraîne VA = VDD. L'armature A subit une variation de +VDD Cette variation est reportée sur l'autre armature (armature B) du condensateur, donc VB passe de VDD/2 à (VDD/2 + VDD) = (3/2)VDD.
2.3. Phase de récupération
|  |
2.4. Les chronogrammes
2.5. Calcul de la durée propre T0
. Appliquons la propriété fondamentale de la fonction exponentielle à Uc sur l'intervalle (t1 à t2)
Avec Uf = VDD ; Ui = 0 ; U0 = VDD/2
Ce qui donne : 
2.6. Calcul de la durée de la phase de récupération TR
On suppose qu'à partir de 3τ le condensateur est totalement déchargé d’où TR = 3.RC
2.6. Vidéo de simulation
