Activité introductrice
Activité introductrice
On considère les fonctions numériques suivantes : \(x\) définie par \(x(t) = sin t\) et \(y\) définie par \(y(t) = cos 2t\)
Question
a) Exprimer 𝑦 en fonction de x.
b) En déduire la nature de la courbe obtenue.
Solution
a) y =1-2x², x ϵ [-1;1].
b) La courbe obtenue est une partie d'une parabole.
On considère le système suivant :
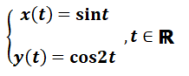
Question
2-a) Que représente ce système pour la courbe obtenue à la question 1. b).
2-b) Déterminer la période commune des fonctions x et y
2-c) En déduire un intervalle d'étude commun aux deux fonctions.
2-d) Etudier la parité des fonctions x et y sur I = [-π ; π]
2-e) En déduire un domaine d'étude pour les deux fonctions
Solution
2. a) Le système est une représentation paramétrique de la parabole de 1.b)
2-b) La période commune de x et y est 2π
2-c) On peut donc étudier x et y sur un intervalle d'amplitude 2π :
soit par exemples [-π ; π] ; [-2π ; 0] ; [0 ; 2π] ;.....
2-d) x est impaire et y est paire.
2-e) On peut étudier les deux fonctions sur l'intervalle J = [0 ; π].