Activité d'introduction
Question
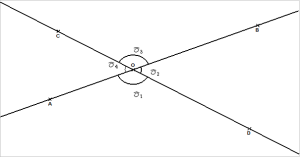
Tracer une droite (AB) puis placer le point O∈[AB]. Construire la droite (CD) sécante à la droite (AB) en O tel que O∈[CD]
a) La figure obtenue admet-elle un centre de symétrie? Si oui, nommez-le.
b) Déterminer les mesures des angles \(\hat{O}_1=\widehat{AOD}\), \(\hat{O}_4=\widehat{AOC}\),
\(\hat{O}_2=\widehat{BOD}\), \(\hat{O}_3=\widehat{BOC}\).
c) Quel constat faites-vous? Justifier la réponse.
Solution
Solution
Figure :
a) La figure d'ensemble obtenue admet un centre de symétrie qui est le point O.
b) Sur cette figure, \(\widehat{AOD}=130^{\circ}\), \(\widehat{AOC}=50^{\circ}\), \(\widehat{BOD}=50^{\circ}\) et \(\widehat{BOC}=130^{\circ}\).
c) Nous constatons que \(\widehat{AOD}=130^{\circ}=\widehat{BOC}\) et \(\widehat{AOC}=50^{\circ}=\widehat{BOC}\).
Justifions la réponse :
La figure d'ensemble admet un centre de symétrie qui est le point O.
L'image de l'angle \(\hat{O}_1=\widehat{AOD}\) par la symétrie centrale de centre O est l'angle \(\hat{O}_3=\widehat{BOC}\) et l'mage de l'angle \(\hat{O}_2=\widehat{BOD}\) est l'angle
\(\hat{O}_4=\widehat{AOC}\).
Dans la symétrie centrale, l'image d'un angle est un angle de même mesure ;
donc \(\hat{O}_1=\hat{O}_3\) et \(\hat{O}_4=\hat{O}_3\).