Éclatement et choc
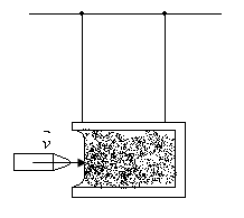
Une balle de fusil, de masse \(m =10\: g,\) arrive à la vitesse de \(600 \:m.s^{-1}\) dans une boîte contenant du sable humide, suspendue par deux fils (voir figure) . La balle s'incruste dans la boîte, dont la masse est \(M = 10 \:kg\).
Question
1) Quelle serait la vitesse de la boîte immédiatement après le choc ?
2) Le fusil qui a tiré la balle a une masse de \(5\: kg\). Calculer la vitesse de recul du fusil dans les deux cas suivants :
a) le fusil, mal épaulé, recule seul ;
b) le fusil, bien épaulé, est solidaire du tireur de masse \(70 \:kg\).
Solution
Le système {boite + balle} est pseudo-isolé. Sa quantité de mouvement se conserve.
1) \({\vec p}_{avant} =m\vec v\) ; \({\vec p}_{apr\grave{e}s}=(M+m)\overrightarrow {v'}\) où \(\vec v\) et \(\overrightarrow {v'}\) sont les vecteurs vitesse respectifs de la balle avant l'impact et de l'ensemble {boîte + balle} après l'impact.
\(m\vec v=(M+m)\overrightarrow {v'}\) soit \(mv=(M+m)v'\) et \(v' = \frac{m}{M+m}v\).
\(v'=\frac{0,01}{10+0,01} \times 600 = 0,6 \:m.s^{-1}\).
La vitesse de la boîte après l'incrustation est \(\bfseries v' = 0,6 m.s^{-1}\)
2) a) Vitesse de recul avec le fusil mal épaulé
\(\vec p_{avant} = \vec 0\) car le système est initialement immobile.
\({\vec p}_{apr\grave{e}s} = M'\overrightarrow {V'}+m\overrightarrow {v'}\) où \(M'\) est la masse du fusil, \(\overrightarrow {V'}\) et \(\overrightarrow {v'}\) sont les vecteurs vitesse respectifs du fusil et de la balle.
\(M\overrightarrow {V'}+m\overrightarrow {v'}=\vec 0\) soit \(M'\overrightarrow {V'}=m\overrightarrow {v'}\). On a donc \(M'V'=mv'\) et \(V' = \frac{m}{M}v'\)
\(v'=\frac{0,01}{5} \times 600 = 1,2 \:m.s^{-1}\).
La vitesse de recul du fusil lorsqu'il est mal épaulé est \(\textbf {v' = 0,6 \:m.s^{-1}}\).
2) b) La vitesse de recul avec le fusil bien épaulé
Le système est constitué d'une part, du tireur et du fusil et d'autre part, de la balle. Notons \(M\) la masse du fusill et du tireur : \(M=70\:kg+5k\: kg = 75 \: kg\).
\({\vec p}_{avant} = \vec 0\) car le système est initialement immobile.
\({\vec p}_{apr\grave{e}s} = M\overrightarrow {V'}+m\overrightarrow {v'}\) où \(\overrightarrow {V'}\) et \(\overrightarrow {v'}\) sont les vecteurs vitesse respectifs du fusil solidaire du tireur et de la balle.
\(M\overrightarrow {V'}+m\overrightarrow {v'}=\vec 0\) soit \(M\overrightarrow {V'}=-m\overrightarrow {v'}\). On a donc \(MV'=mv'\).
\(V' = \frac{m}{M}v'\)
\(V'=\frac{0,01}{75} \times 600 = 0,08 \:m.s^{-1}\).
La vitesse de recul du fusil lorsqu'il est bien épaulé est \(\textbf{V' = 0,08 \:m.s^{-1}}\)