Exercice : Choc élastique [Applications du principe de l'inertie]

Choc élastique

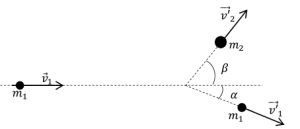
Un projectile de masse m₁ = 100 g glisse sur la surface d'un lac gelé (horizontal) et rencontre une pierre de masse m₂ = 70 g qui est immobile. Le projectile rebondit sur la pierre, sa nouvelle direction faisant un angle α = 30 ° avec la direction de sa trajectoire initiale, tandis que la pierre part dans une direction faisant un angle β = 50 ° avec la direction initiale du projectile (voir figure).

La vitesse du projectile avant le choc est v'₁ = 10 m.s^-1.

Question

Calculer sa vitesse v^'₁' et celle de la pierre v'_2' après le choc.

Solution

Le projectile et la pierre sont soumis chacun à son poids et à la réaction de la surface du lac. Les frottements étant négligeables, la réaction est normale et compense le poids. Le système constitué par la pierre et le projectile est donc pseudo-isolé. D. Son vecteur quantité de mouvement est constant : ${\vec{p}}_{avant} = {\vec{p}}_{après}$ soit $\vec{p_{1}} = {\vec{p}}_{1}' + {\vec{p}}_{2}'$ car la pierre est initialement immobile. Les caractéristiques de ${\vec{p}}_{1}$ et de $\vec{p_{1}'}$ étant connues, il s'agit de construire ${\vec{p}}_{2}'$ tel que :

$\vec{p_{1}} = {\vec{p}}_{1}' + {\vec{p}}_{2}'$ .

Projetons cette dernière relation sur la direction de ${\vec{v}}_{1}$ : $p_{1} = p_{1}' \times \cos (α) + p_{2}' \times \cos (β)$

Projetons-la ensuite sur la direction orthogonale à ${\vec{v}}_{1}$ : $0 = - p_{1}' \times \sin (α) + p_{2}' \times \sin (β)$ .

p₁= m1.v1 = 0,1 x10 = 1 Kg.m.s-1 ; p'₁x cos(α) = 0,1 x v'1 x cos(30) = 0,0866v'1 ; p'₁xsin(α) = 0,1xv'₁xsin(30)=0,05v'1 ; p'2xsin(β)=0,07xv'2xsin(50) = 0,0536v'2.

Par remplacement, on obtient le système suivant : ${\begin{matrix} 0,0866 v_{1}' + 0,045 v_{2}' = 1 \\ 0,05 v_{1}' - 0,0536 v_{2}' = 0 \end{matrix}$

La résolution de ce système d'équation donne v'₂=7,3 m.s-1.

De la dernière projection, on tire ${\vec{p}}_{2}'$ que l'on remplace dans la première projection. on obtient :

Remarque :

Des projections, on tire : ${\begin{matrix} p_{1}' \times \sin (α) = p_{2}' \times \sin (β) \\ p_{1}' \times \cos (α) = p_{1} - p_{2}' \times \cos (β) \end{matrix}$

Par division membre à membre, on élimine p'₁ et on obtient $p_{2}' = \frac{p_{1} \times \tan (α)}{\tan (α) \times \cos (β) + \sin (β)}$ soit

$v_{2}' = \frac{p_{1} \times \tan (α)}{m_{2} ⟦ \tan (α) \times \cos (β) + \sin (β) ⟧}$

$v_{2}' = \frac{0,1 \times 10 \times \tan (30 °)}{m_{2} ⟦ \tan (30) \times \tan (50 °) + \sin (50 °) ⟧} = 7,25 m . s^{- 1}$