Exercice : Choc mou [Applications du principe de l'inertie]

Choc mou

Par un jour d'hiver, les chaussées sont glissantes et l'on suppose que les véhicules qui s'y déplacent sont des solides pseudo isolés.

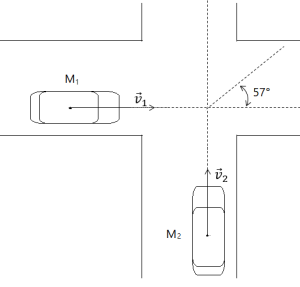
Deux automobiles se heurtent au croisement de deux routes perpendiculaires et horizontales (voir figure). La première, de masse $m_1 = 1000 \:kg$, roulait à la vitesse $v_1 = 40 \:km.h^{-1}$. La deuxième, de masse $m_2 = 800 \:kg$, se déplaçait à la vitesse $v_2$.

Après le choc, les deux automobiles restent accrochées et la direction prise par l'ensemble forme un angle α = 57° avec la direction initiale du premier véhicule.

Question

La vitesse maximale autorisée sur ces deux routes étant de $45 km.h^{-1}$, le conducteur du deuxième véhicule était-il en infraction pour excès de vitesse ?
Représente la trajectoire du centre d'inertie du système des deux véhicules (avant et après le choc).

Solution

Les frottements étant négligeables, la réaction du sol lui est perpendiculaire. Chaque véhicule est soumis à son poids et à la réaction du sol. Ces deux forces sont opposées : $\vec{P} + \vec{R} = \vec{0}$ . Le système constitué des deux véhicules est pseudo-isolé. Le vecteur quantité de mouvement dans le référentiel terrestre (considéré comme galiléen) est contant.

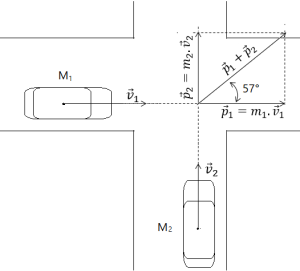
La quantité de mouvement avant le choc est : ${\vec{p}}_{avant} = {\vec{p}}_{1} + {\vec{p}}_{2} = m_{1} \cdot {\vec{v}}_{1} + m_{2} \cdot {\vec{v}}_{2}$

La quantité de mouvement après le choc est :$ {\overrightarrow p}_{apr\grave e s}=(m_1+m_2) \cdot \vec v$.

Comme le vecteur vitesse et le vecteur quantité de mouvement ont la même direction, on peut dire que le vecteur quantité de mouvement du système des deux véhicules après le choc fait également un angle de 57° avec la direction initiale de la trajectoire du premier véhicule. Les directions de ${\vec{p}}_{1}$ et de ${\vec{p}}_{2}$ sont connues et sont perpendiculaires ; la norme de ${\vec{p}}_{1}$ est également connue. Il faut alors construire ${\vec{p}}_{2}$ de sorte que la direction de la somme ${\vec{p}}_{1} + {\vec{p}}_{2}$ fasse un angle de 57° avec la direction de ${\vec{v}}_{1}$ .

À partir de la figure, on a : $\tan (57 °) = \frac{p_{2}}{p_{1}} = \frac{m_{2} \cdot v_{2}}{m_{1} \cdot v_{1}}$ soit $v_{2} = \frac{m_{1} \cdot v_{1} \cdot \tan (57 °)}{m_{2}}$

$v_1 = 40 \:km.h^{-1}=11,11 \:=m.s^{-1}$

$v_{2} = \frac{1000 \times 11,11 \times \tan (57 °)}{800}$

$v_2= 21,39 \: m.s^{-1}$ soit $v_2= 77 \: km.h^{-1}$.

La vitesse du deuxième véhicule est supérieure à la vitesse maximale autorisée qui est de 45 km.h^-1. Son conducteur était donc en infraction pour excès de vitesse.

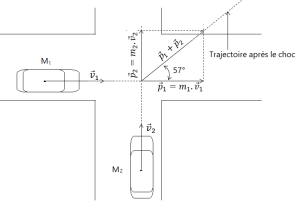
Trajectoire après le choc

Le système formé par les deux véhicules étant pseudo-isolé, la trajectoire de son centre d'inertie est rectiligne durant tout le mouvement du système. La trajectoire du centre d'inertie des deux véhicules est donc une droite faisant un angle de 57° avec la direction de la vitesse du premier véhicule.